Multiply each term in y z = x y z = x by z z Cancel the common factor of z z Tap for more steps Cancel the common factor Rewrite the expression Rewrite the equation as x z = y x z = y Divide each term by x x and simplify Tap for more steps Divide each term in x z = y x z = y by x xThis 3 equations 3 unknown variables solver computes the output value of the variables X and Y with respect to the input values of X, Y and Z coefficients In mathematic calculations, there are many situation arises where the usage of equation containing 3 unknown variables need to be solved prior to go further with the calculations Click here 👆 to get an answer to your question ️ what is the formula of (xyz)^3 chax chax Math Secondary School answered What is the formula of (xyz)^3 1 See answer chax is waiting for your help Add your answer and earn points

X Y Z 3 Formula Novocom Top
How to solve for x y and z with 3 equations
How to solve for x y and z with 3 equations-Get the answer to this question and access a vast question bank that is tailored for students(xyz)^3 formula
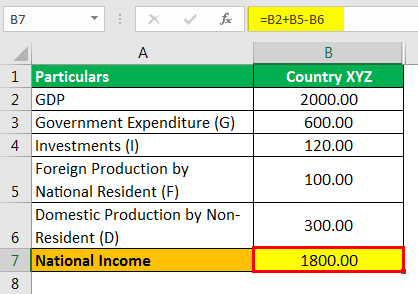



National Income Formula Step By Step Calculation Methods Examples
(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x^2y 3xy^2 3 ( x^2 y^2 2xy ) z 3x z^2 3yz^2 =x^3y^3z^3 3x^2 y3xy^2 3x^2More formally, the number of k element subsets (or k combinations) of an n element set This number can beMathematics Menu The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeFormula This is the formula that we are going to use to solve any linear equations X = A⁻¹ B Example 1 Solve the following linear equation by inversion method 2x y 3z = 9 x y z = 6 x y z = 2 Solution First we have to write the given equation in the form AX = B Here X represents the unknown variablesIf xy=z Then x^3y^3z^33xyz=?
Why create a profile on Shaalaacom?Quote Investigator In 1929 Albert Einstein was interviewed by Samuel J Woolf in Berlin for a piece published in "The New York Times Magazine" What is the formula for the variance of 3 dependent variables?




Art Of Problem Solving




X Y Z 3 Formula Novocom Top
= X 3 Y 3 Z 3 3XY 3YZ 3XZ 8 ;Using the above identity taking a = x−y, b = y−z and c= z−x, we have abc= x−yy−zz −x= 0 then the equation (x− y)3 (y−z)3 (z−x)3 can be factorised as follows (x−y)3 (y−z)3 (z−x)3 = 3(x−y)(y−z)(z−x) Hence, (x−y)3 (y−z)3 (z −x)3 = 3(x−y)(y −z)(z −x) Answer verified by Toppr(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yz




Formula X Y Math Formulas




X Y Z 3 Formula Novocom Top
Please do not give me the general formula for n number of variables I've seen it but I don't understand it(xy) (xz) (yz) = (xyz) (xyyzxz)xyz x 2 y 2 z 2 = (xyz) 2 2(xyyzxz) x 3 y 3 z 3 = (xyz)(x 2 y 2 z 2xyxzyz) Apparently, he also fashioned a lesswellknown humorous formula about success in life using the terms A, X, Y, and Z Did Einstein actually craft this quasimathematical joke?



1



Plos One Excellent Accuracy Of Abc 2 Volume Formula Compared To Computer Assisted Volumetric Analysis Of Subdural Hematomas
View Full Answer thats corect6 ;In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial)For example, is a quadratic form in the variables x and yThe coefficients usually belong to a fixed field K, such as the real or complex numbers, and one speaks of a quadratic form over KIf =, and the quadratic form takes zero only when allL #shorts l Algebra Identities l algebra l Algebra formula l math lHow to solve If xy=z Then x^3y^3z^33xyz=?




Solving A Non Linear System Of Equations In Python Using Newton S Method Stack Overflow




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In
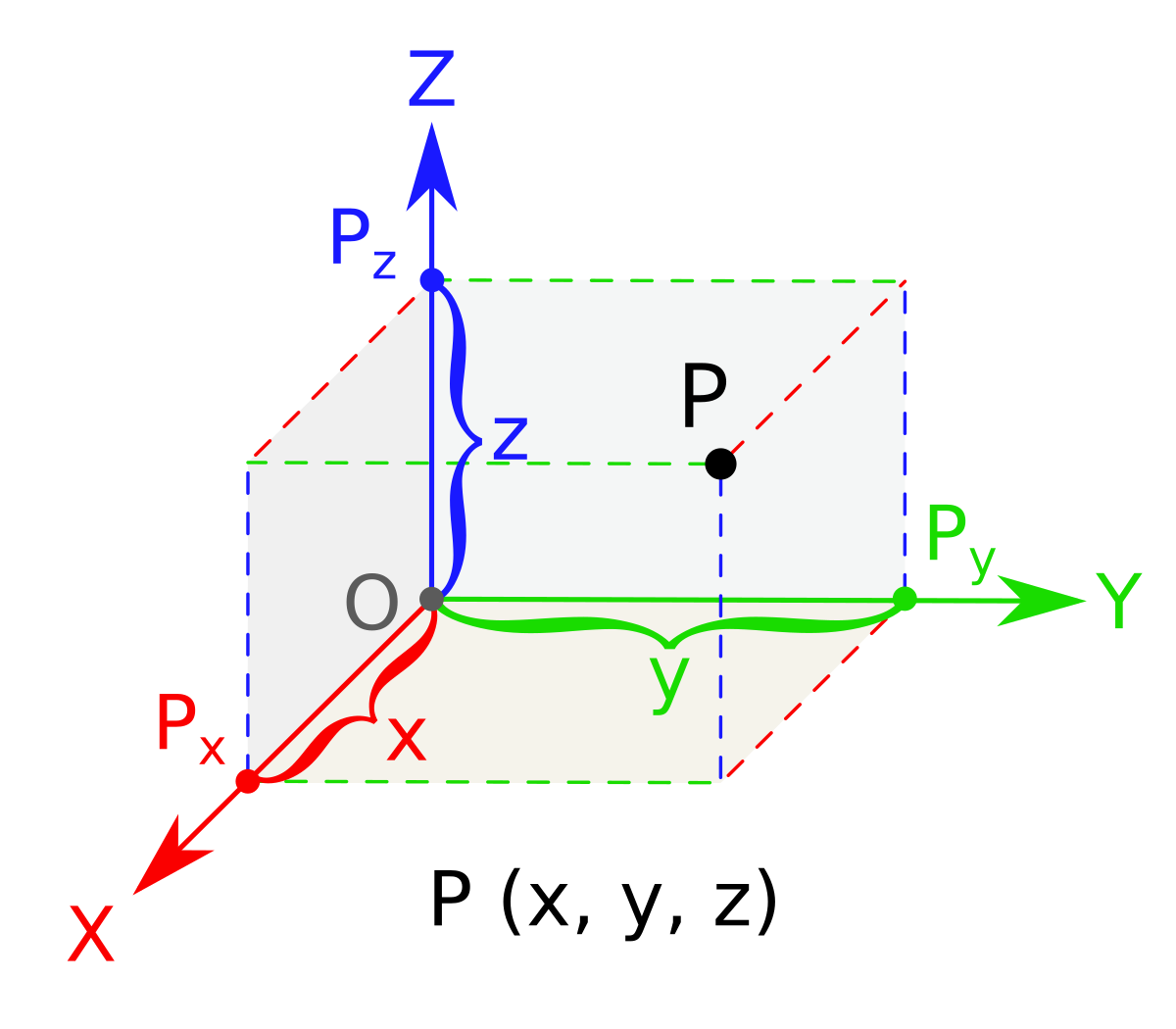
The distance between two points is the length of the path connecting them The shortest path distance is a straight line In a 3 dimensional plane, the distance between points (X 1, Y 1, Z 1) and (X 2, Y 2, Z 2) is given by \ d = \sqrt {(x_{2} x_{1})^2 (y_{2} y_{1})^2 (z_{2} z_{1})^2} \ What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?X 2 y 2 = r 2 This is just an algebraic way of stating the Theorem of Pythagoras For a sphere you need to use Pythagoras' theorem twice In the diagram below O is the origin and P (x,y,z) is a point in 3space P is on the sphere with center O and radius r if and only if the distance from O to P is r The triangle OAB is a right triangle and




Solve The Following System Of Equation By Matrix Method 1 X Y Z 6 X Y Z 4 X 2y 2z 1 2 X Y 3z 10 X Y Z 2 2x 3y 4z 4 3 X Y Z 6 X 2y 3z 6 X Y Z 2 4 2x Y Mathematics Topperlearning Com Yv1op566




X Y Z 3 Formula Novocom Top
1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials informationThe formula of x 3 y 3 z 3 – 3xyz is written as \(x^{3} y^{3} z^{3} – 3xyz = (x y z) (x^{2} y^{2} z^{2} – xy – yz – zx)\) Let us prove the equation by putting the values of Algebra Formulas A basic formula in Algebra represents the relationship between different variables The variable could be taken as x, y, a, b, c or any other alphabet that represents a number unknown yet Example – (x y = z) (a b)2=a2 2ab b2 (a−b)2=a2−2ab




X Y Z 3 Formula Novocom Top




Let O X Y X In R 3 Xyz 1 And Define G Chegg Com
If you know that z is linear in x and y, you can use LINEST to get the coefficients For example, if x and y are in col A & B, and z in col C, then select a threecell wide range and arrayenter the formula =LINEST (C1C, A10) You have a tabulated list of x, y, and z values, and want a formula that expresses z as a function of x and y?Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)



Www Jstor Org Stable




Solved 3 Let G R3r Be Given By The Formula G X Y Z 2y Chegg Com
X^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and #x^3y^3z^33xyz=x^3y^33x^2y3xy^2z^33xyz3x^2y3xy^2=(xy)^3z^33xy(xyz)=(xyz)((xy)^2z^2(xy)z)3xy(xyz)=(xyz)(x^22xyy^2z^2xyxz3xy)=(xyz)(x^2y^2z^2xyyzzx)# Answer link Related questionsBy using this list of formulas on 3D Coordinate Geometry concepts, you can understand and solve basic to complex ThreeDimensional Coordinate Geometry problems easily and quickly 1 Distance between two points If P (x 1, y 1, z 1) and Q (x 2, y 2, z 2) are two points, then distance between them PQ = ( x 1 − x 2) 2 ( y 1 − y 2) 2 ( z




Formula Of X Y Z 3 Novocom Top




What Is The Formula Of Math A B 3 Math Quora
' 3 δx x δz z −4 δy y, where δx x = − 3 100, δy y = 1 100 and δz z = 2 100 Hence, δw w ×100 = −92−4 = −13 Thus, w is too small by approximately 11%, as before 2 In the formula w = v u u u u u t x3 y, x is subjected to an increase of 2% Calculate, approximately, the percentage change needed in y to ensure that w remains unchanged Solution lnw = 1 2 3lnx−lny Hence, 11X y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2IF X 1/ 3 Y 1/ 3 Z 1/ 3=0 THEN FIND THE VALUE OF X 3 Y 3 Z 3 1 (xyz) whole cube =x cubey cube zcube 3xy3yz3zx2 THE EXPANSION OF x 3 y 3 z 3 = x 3 y 3 z 3 3(xy)(yz)(xz) 3



Formula For X Y Z 2 Brainly In




What Are Various Forms To Write A B C A Whole Cube Quora
W = f(x;y;z) where x, y and z are the independent variables For example, w = xsin(y 3z) Partial derivatives are computed similarly to the two variable case For example, @w=@x means difierentiate with respect to x holding both y and z constant and so, for this example, @w=@x = sin(y 3z) Note that a function of three variables does not In First value of Y In A3 =the formula (X,Y) In a way Excel can calculate it like in your question =A1^2^2 In >F3 for example write X values In >A10 for example write Y values Select A3F10 Clickon Data Table in Data Tab In Row Input Cell write A1 In Column Input Cell write Click Ok This says that the gradient vector is always orthogonal, or normal, to the surface at a point So, the tangent plane to the surface given by f (x,y,z) = k f ( x, y, z) = k at (x0,y0,z0) ( x 0, y 0, z 0) has the equation, This is a much more general form of the equation of a tangent plane than the one that we derived in the previous section




X 3 Y 3 Z 3 Xyz Novocom Top



What Is The Value Of X Y Z Where Xyz Xy Xz Yz X Y Z 3 Quora
If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____Find an answer to your question formula of (xyz)^3 1 Log in Join now 1 Log in Join now Ask your question sumitsaraf1984 sumitsaraf1984 Math Secondary School Formula of (xyz)^3 2X 2 a 2 y 2 a 3 z 2 a 4 xya 5 xza 6 yz then q is called a quadratic form (in variables x,y,z) There i s a q value (a scalar) at every point (To a physicist, q is probably the energy of a system with ingredients x,y,z) The matrix for q is A= a 1 1 2 a 4 1 a 5 1 2 a 4 a 2 1 2 a 6 1 2 a 5 1 2 a 6 a 3 It's the symmetric matrix A with this




Warm Up Evaluate For X 2 Y 3 And Z 1 1 X2 2 Xyz 3 X2 Yz Ppt Download




The Formula For Luck Leave Nothing To Chance Ten Powerful Principles For Building A Luck Mindset Lacey Stuart Ismail Salim Amazon Com Books
3 Answers3 The general formula for the Taylor expansion of a sufficiently smooth real valued function f R n → R at x 0 is In these formulas, ∇ f is the (first) gradient of f and ∇ ∇ f is usually called the Hessian (second gradient) of f You can extend this formulation for functions like f R nWhat is the formula for (xyz) ^2? 0 Mithra, added an answer, on 23/9/ Mithra answered this (xyz) 2 = x 2 y 2 z 2 2xy 2yz2zx Was this answer helpful?
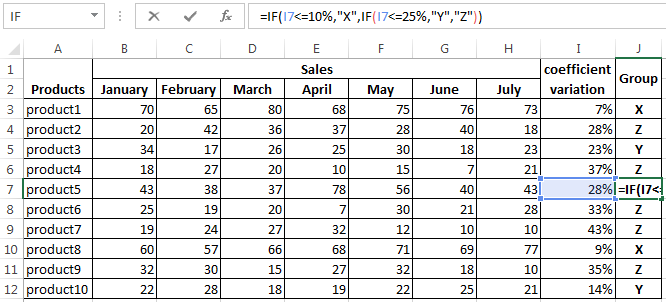



Abc And Xyz Analysis In Excel With Example Of Calculation




National Income Formula Step By Step Calculation Methods Examples
This formula returns "x" if the color in B5 is either "red" or "green", and the quantity in C5 is greater than 10 Otherwise, the formula returns an empty string ("") Explanation In the example shown, we want to "mark" or "flag" records where the color is either red OR green AND the quantity is greater than 10For 2 dependent variables, the formula is Var(X)Var(Y)2*Cov(X,Y) What is Var(XYZ) if the variables are dependent?Y = r 2 x − c 2 From the upper diagram we see that S 1 and S 2 are the foci of the ellipse section of the ellipsoid in the xzplane and that r 2 z = r 2 x − a 2 Converse If, conversely, a triaxial ellipsoid is given by its equation, then from the equations in step 3 one can derive the parameters a, b, l for a pinsandstring construction



Www Usna Edu Users Oceano Raylee Sm223 Ch12 1 Stewart 16 Pdf




Holt Algebra 1 9 9 The Quadratic Formula And The Discriminant Warm Up Add To Hw Pass Back Papers Evaluate For X 2 Quadratic Formula Quadratics Algebra 1
∗) (valid for any elements x , y of a commutative ring), which explains the name "binomial coefficient" Another occurrence of this number is in combinatorics, where it gives the number of ways, disregarding order, that k objects can be chosen from among n objects;There are two formula of it x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2}Transposition of simple formulae 3 4 The formula for the simple pendulum 5 5 Further examples of useful formulae 6 wwwmathcentreacuk 1 Suppose we wish to rearrange y(2x1) = x 1 in order to find x Notice that x occurs both on the left and
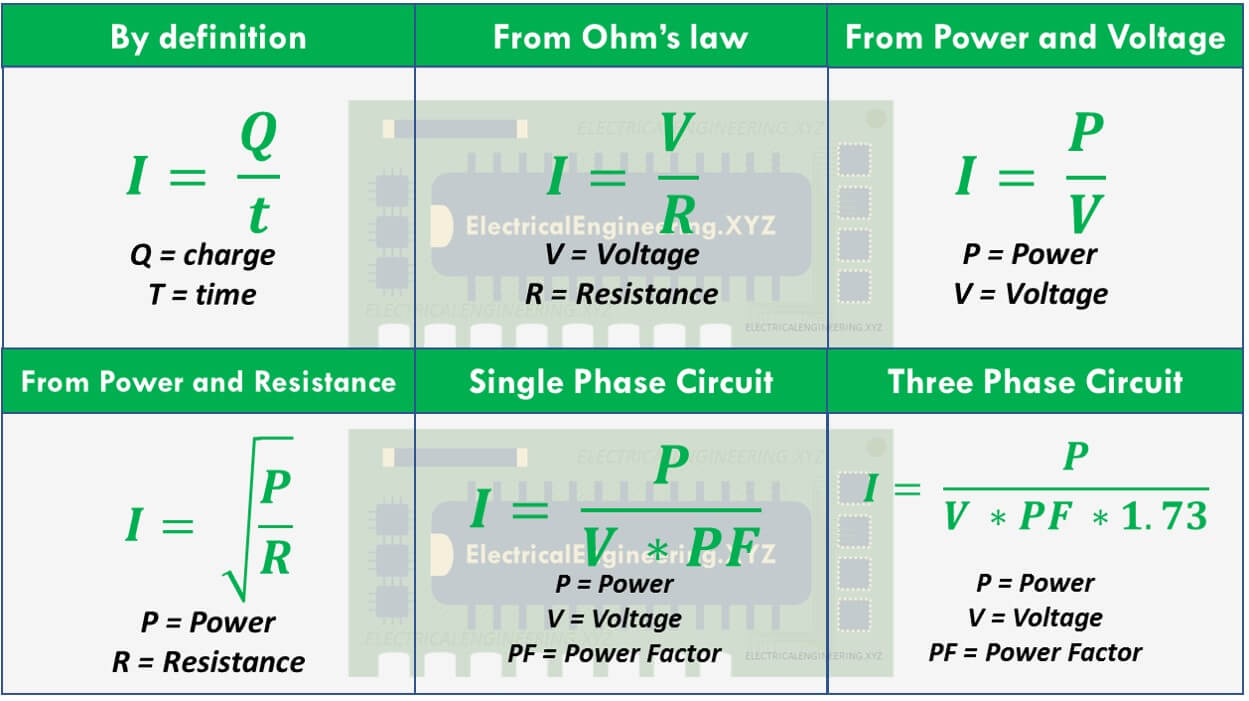



Electric Current Formula Electricalengineering Xyz Formulas




What Is The Value Of Math X 4 Y 4 Z 4 Math Given That Math X Dfrac Yz Y Dfrac Zx Z Dfrac Xy 1 Math Quora
The chain rule for this case is, dz dt = ∂f ∂x dx dt ∂f ∂y dy dt d z d t = ∂ f ∂ x d x d t ∂ f ∂ y d y d t So, basically what we're doing here is differentiating f f with respect to each variable in it and then multiplying each of these by the derivative of that variable with respect to t tTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `xyz=1,x yy zz x=1`and `x y z=1,`find the value of `x^3y^3z^3dot` #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#
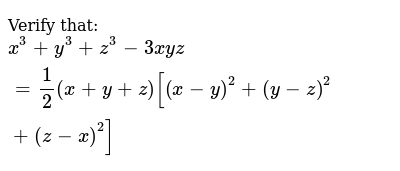



8y Z 4 9xyz 27 5x Y Verify It When X 1 Y 1 Z 2




X Y Z 3 Formula Novocom Top
Using the identity and proof x^3 y^3 z^3 3xyz = (x y z) (x^2 y^2 z^2 xy yz zx)
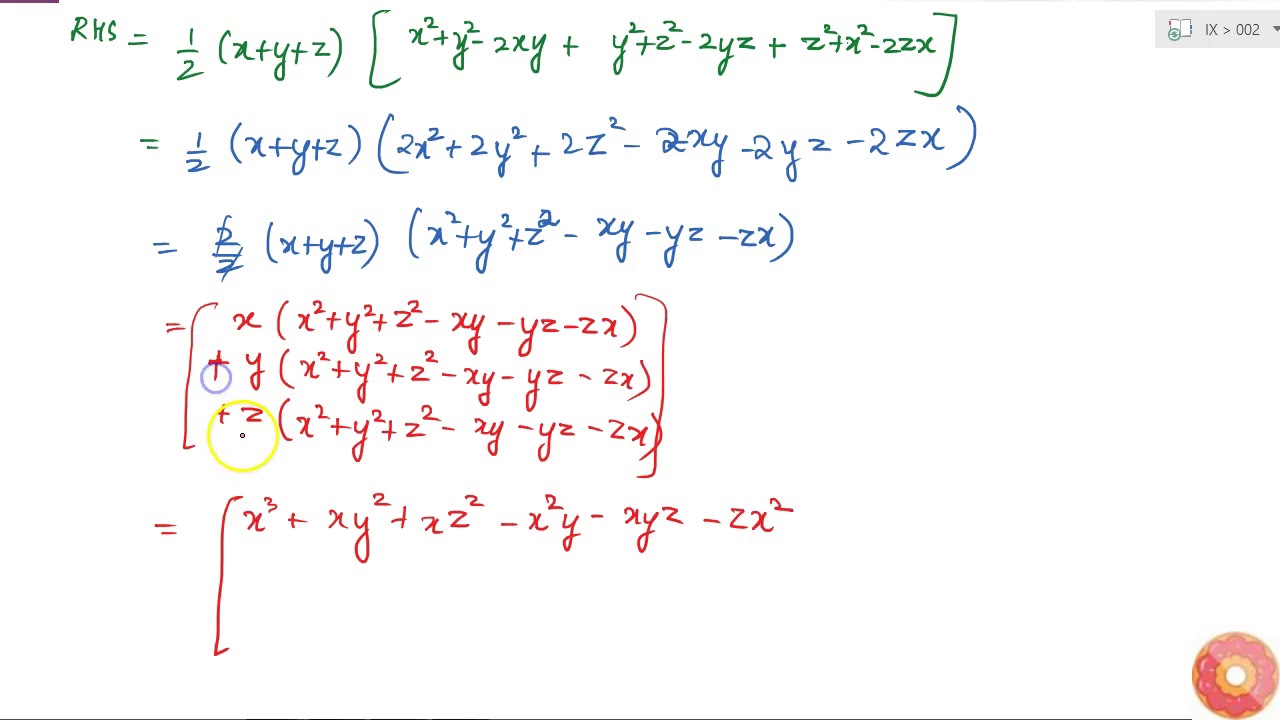



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




106 Chapter




Solve The Following System Of Linear Equations Using Matrix Method 2x Y Z 7 3x Y Z 7 X Y Z 3 Mathematics Topperlearning Com Dzzybtzz
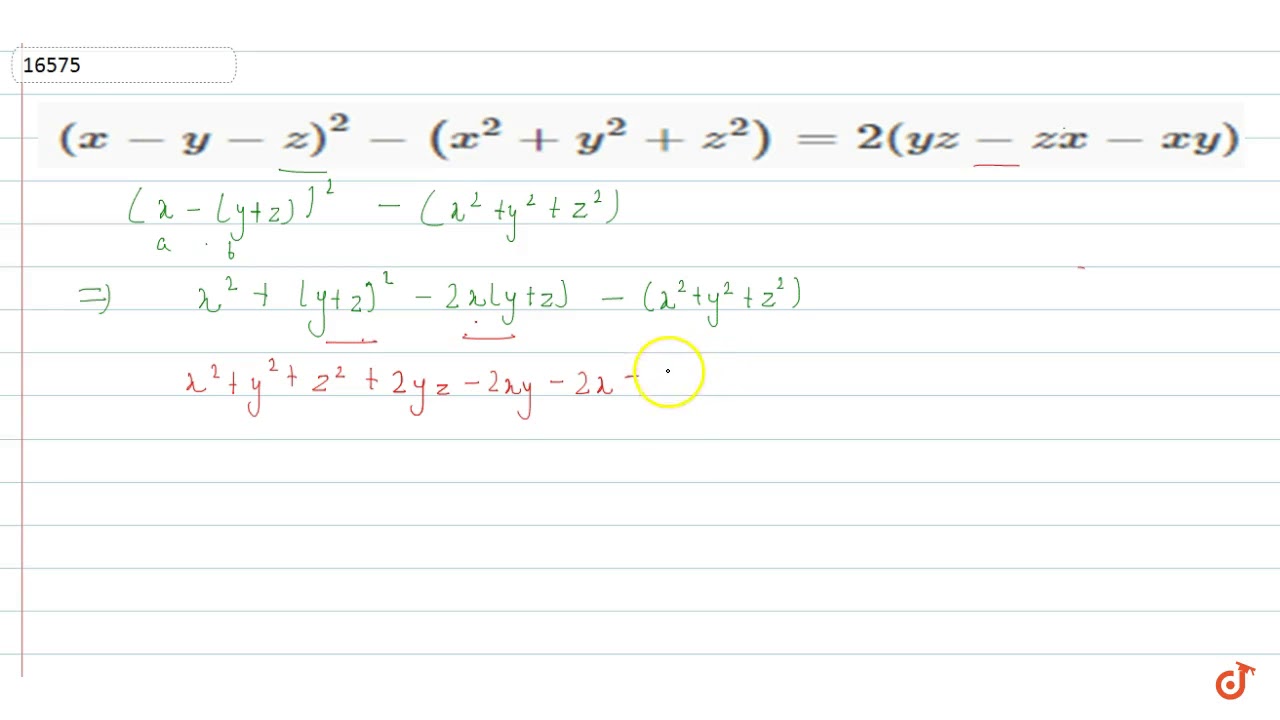



X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube




A Denotes The Product Xyz Where X Y And Z Satisfy Log 3 X Log5 Log7 And Log 5 Y Log7 Log 3 And Log 7 Z Log 3 Log5 B Denotes The Sum Of Square Of Solution Of The Equation



Equations Of Lines And Planes




How To Graph Xyz Data In 3d Inside Microsoft Excel Gray Technical Llc




Maths Xyz Formula Math Formulas



Three Dimensional Space Wikipedia




Ln Delta Xyz Mangle Y Xy 10 And Xz 11 Gauthmath



Production Of X From Y And Other Z Is Called Ammonification




A The Equation Xyz E Y Z 3 Defines Z Chegg Com



Recruiters Tips Using The X Y Z Formula On Your Resume Math Online Tom Circle




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




X Y Z 3 Formula Novocom Top




Formula According To Blender To Create An Enneper Order 3 Blender Stack Exchange



1




The Xyz Formula Drs Les And Leslie Parrott Marriage Missions International
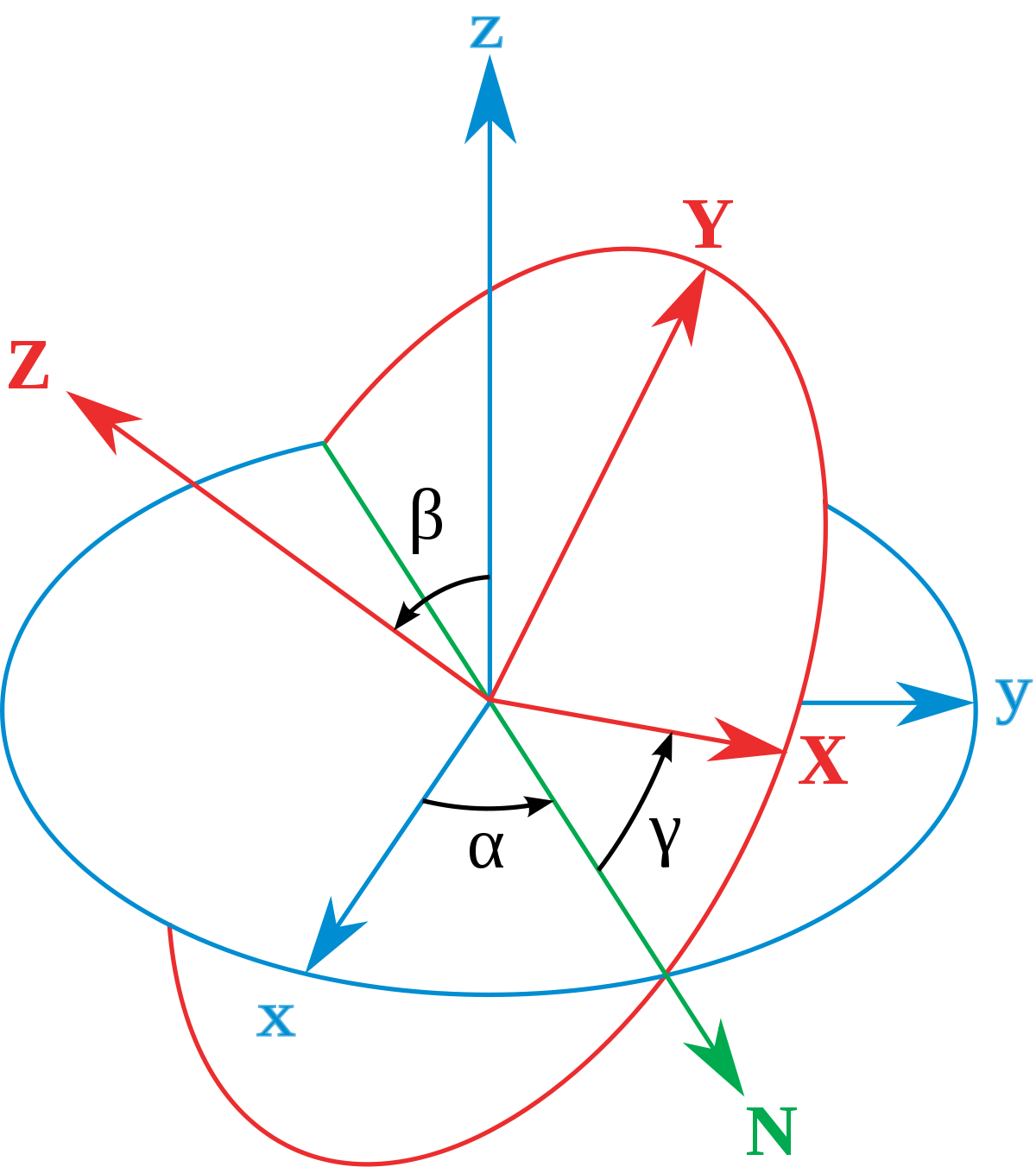



Euler Angles Wikipedia




X Cube Y Cube Z Cube Minus 3 X Y Z Brainly In




Maths Xyz Formula Math Formulas
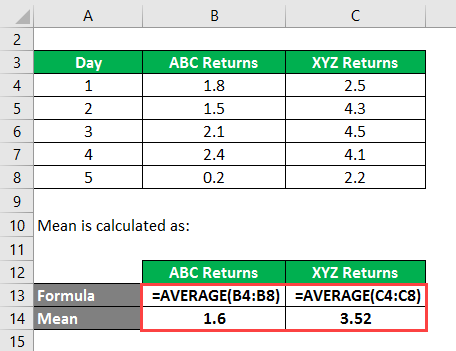



Covariance Formula Examples How To Calculate Correlation




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Mathematical Derivation Of The Abc 2 Formula From A Half Ellipsoid Download Scientific Diagram




Formula According To Blender To Create An Enneper Order 3 Blender Stack Exchange



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University
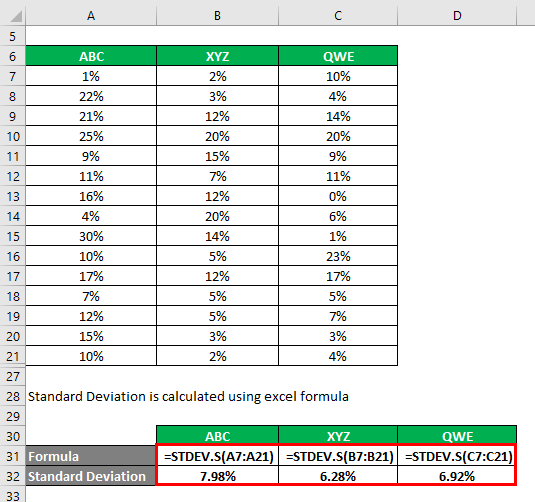



Coefficient Of Variation Formula Calculation With Excel Template




Polynomials Ppt Video Online Download



The Three Dimensional Coordinate System



F Test Formula How To Calculate F Test Examples With Excel Template




A Crystal Is Made By Using Particles X Y And Z Particle Z Forms Ccp




Right Triangle Xyz Has Vertices X 1 4 And Y 2 3 The Vertex Z Has Positive Integer Coordinates And X 5 Find The Coordinates Of Z And Solve Xyz Give Exact Answers Study Com
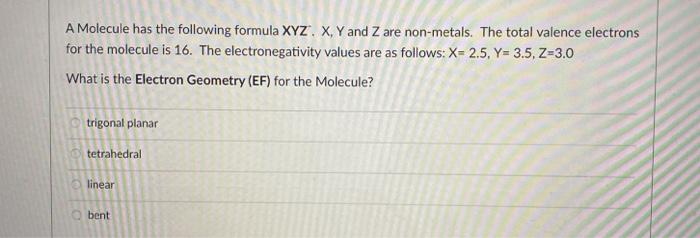



A Molecule Has The Following Formula Xyz X Y And Z Chegg Com



Solution The No Of Solution Of X Y Z To The System Of Equations X 2y 4z 9 4yz 2xz Xy 13 Xyz 13 Such That At Least Two Of X Y Z Are Integers Is A 3 B 5 C 6 D 4




Lesson 9 8 Warm Up Evaluate For X 2 Y 3 And Z X 2 2 Xyz 3 X 2 Yz4 Y Xz 4 5 X 6 Z 2 Xy Ppt Download



How To Prove That Math X Y Z 3 27xyz Geq0 Math Quora




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55



Solution Points A 1 0 B 3 7 And C 5 2 Are The Midpoints Of The Sides Yz Zx And Xy Of Triangle Xyz Find The Equation Of The Line Xy




The Distance And Midpoint Formulas Goal 1 Find




Find The Value Of X Cube Y Cube Z Cube Minus 3 X Y Z If X Square Y Square Z Square Is Equal To Brainly In
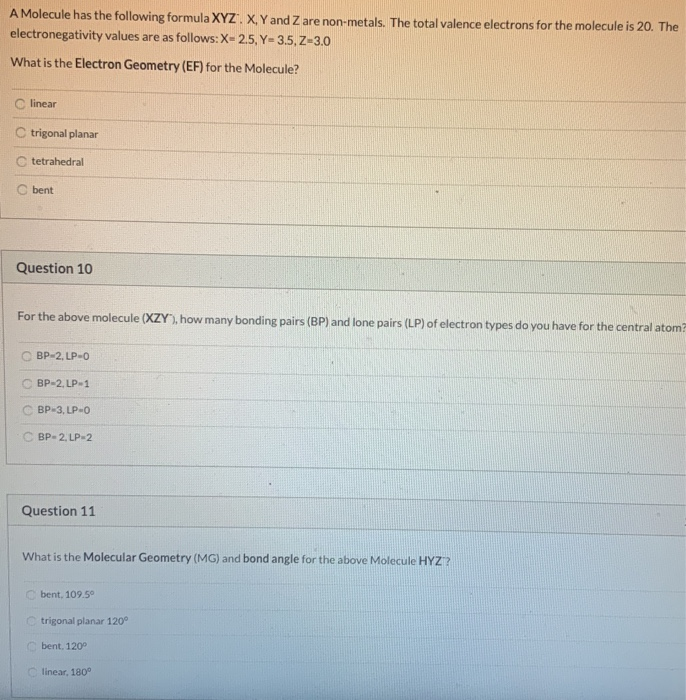



A Molecule Has The Following Formula Xyz X Y And Z Chegg Com




Definition Of X Y Z Matrix Pcmag




Solved Given Z Xyz Et 2 Uv Y V2 3 Z C Chegg Com




What Are Various Forms To Write A B C A Whole Cube Quora
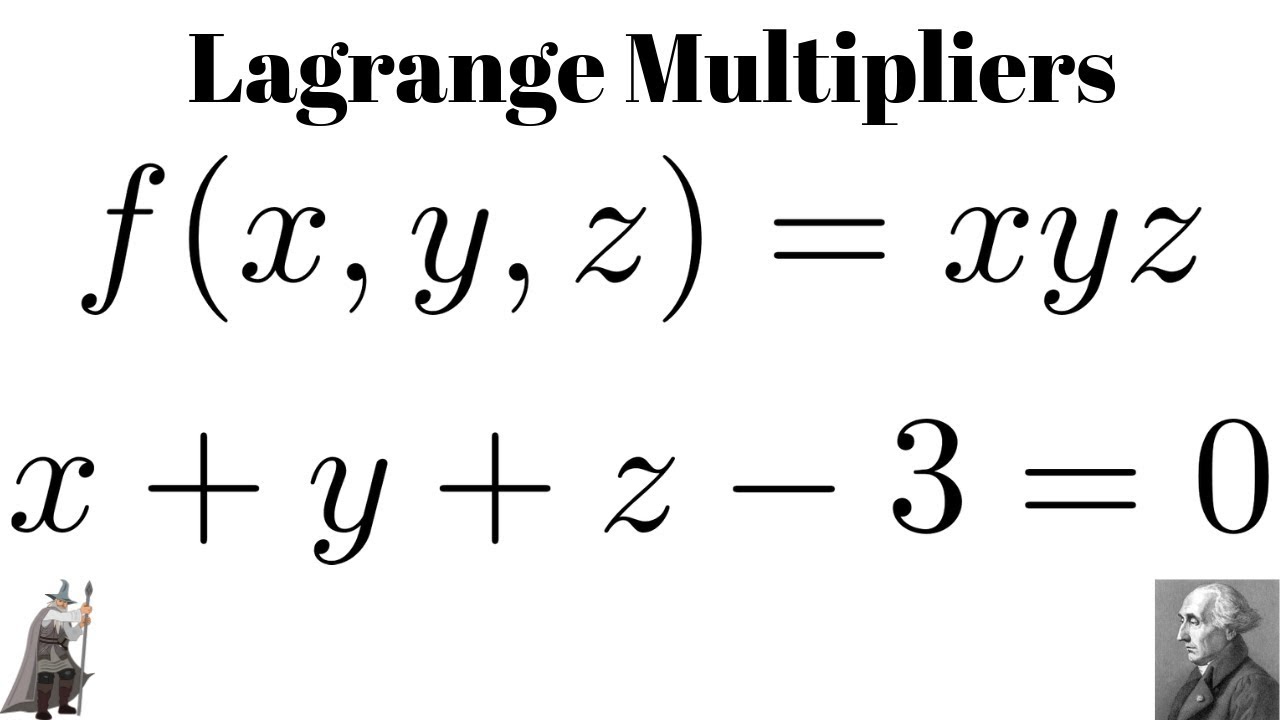



Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube




Equation Of A Sphere Expii




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download




90 3 2 1 Mol 4 2 4 Mol If Three Elements X Y And Z Crystallise In




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




Formula Of X Y Z 3 Novocom Top




You The Chemistry Detective Have Obtained A Water Insoluble Ionic Compound With The Formula Xyz3 Where X Homeworklib




Google Recruiters Say Using The X Y Z Formula On Your Resume Will Improve Your Odds Of Getting Hired At Google Inc Com




Lesson 9 8 Warm Up Evaluate For X 2 Y 3 And Z X 2 2 Xyz 3 X 2 Yz4 Y Xz 4 5 X 6 Z 2 Xy Ppt Download




Solved 1 Calculate Breakeven Sales Dollars For Xyz Compa Chegg Com




How To Calculate Current From Hp Electrical Engineering Xyz Formulae
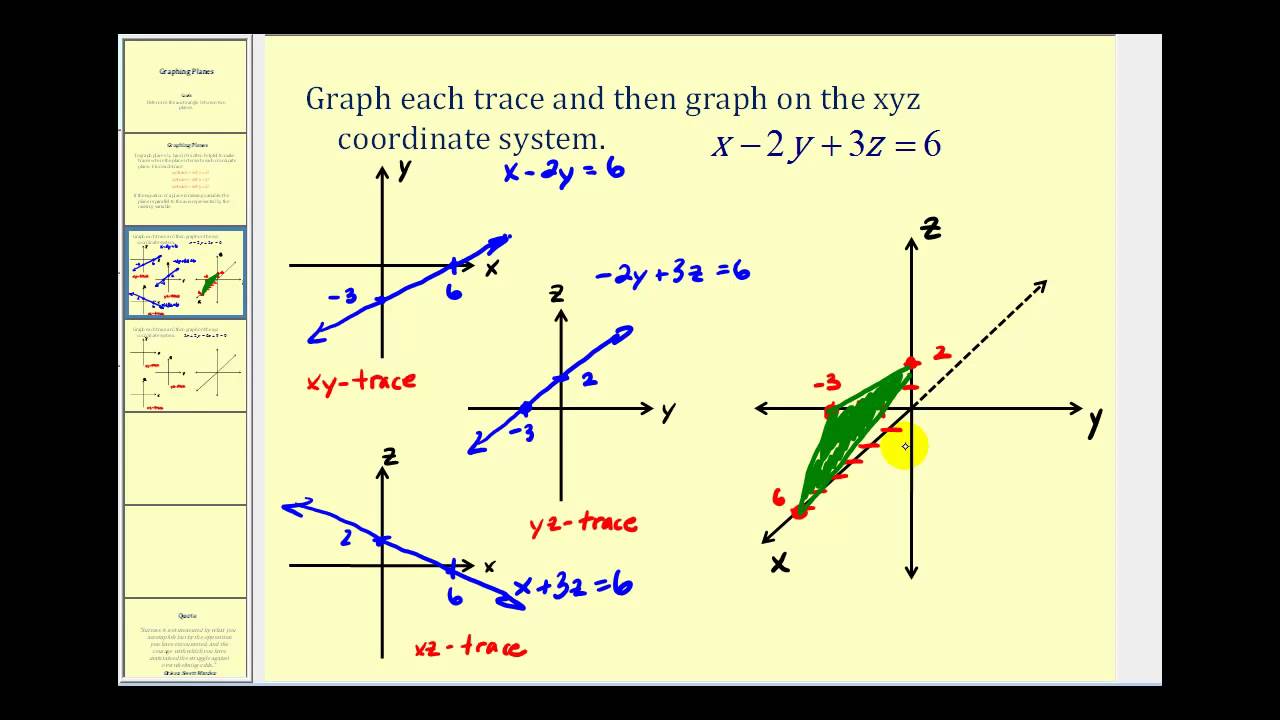



Graphing A Plane On The Xyz Coordinate System Using Traces Youtube




Formula X Y Math Formulas




Question 14 Xyz Company Uses The Formula Y A Bx To Predict And Analyze Homeworklib




Chapter 9 Xyz Custom Plus
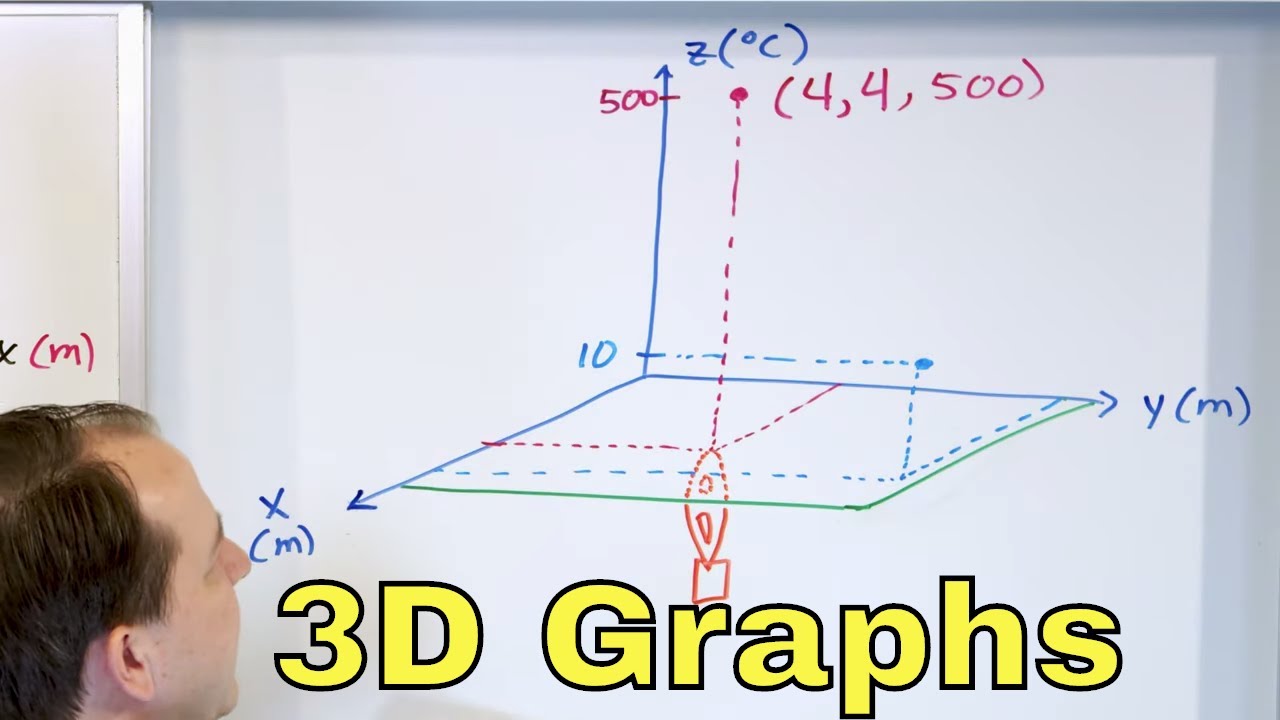



11 Graphing Points In 3d Intro To 3d Functions 3d Coordinates Xyz System Youtube




X Y Z 3 Formula Novocom Top



1




X Y Z 3 Formula Novocom Top




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




Gallery Of Xyz Formula Wgnb 3




Crystal Would Be 1 Xyz 18 2 X Yz2 4 X Y Z 1 Closest Only 3 Formula An Ionic Compound Ab Has Naci Type 3 X Y Z5 Structures If The Radius Of




Find The Value Of X Y And Z Calculator
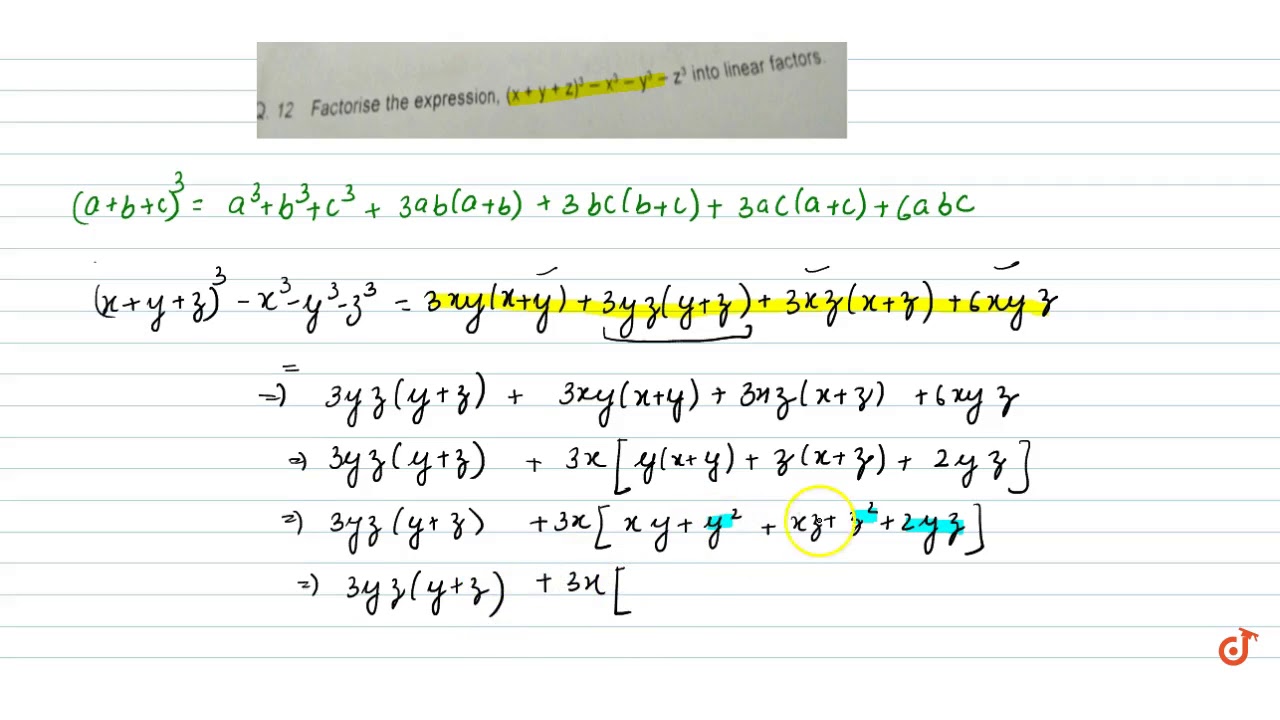



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




Jacobian In Three Variables To Change Variables Krista King Math Online Math Tutor
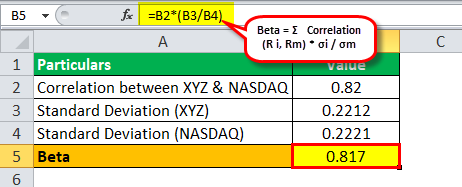



Beta Formula Top 3 Methods Step By Step Examples To Calculate Beta




How To Create Cross Section With Coordinates Xyz Nez Calculation Wi




Bits Of Math Problem Cubes And Cube Roots



0 件のコメント:
コメントを投稿